Trick to count how many Squares/Triangles in a figure

The problem of counting the number of squares on a checkerboard is a classic. This activity begins
with the embedded-square problem and offers several extensions. As students work through these problems, they should appreciate the importance of systematically organizing their data.
Pose the following problem to the students:

How many squares are on a checkerboard?

If students are not familiar with a checkerboard, it would be helpful to have one on hand. Some students may only count the individual small squares on the checkerboard and use that number as their final answer. Others will recognize squares of varying size.
While students are thinking about the problem, distribute the Shape Templates activity sheet for students to cut out the squares.
Shape Templates Activity Sheet
Teacher Notes
The following activities may span several class periods. Students may work in groups to complete these activities.
To help students who struggle with visualization skills, allow them to work in groups. Thus, a field-independent person can guide a field-dependent person to see the embedded figure, for instance, by tracing the figure on the paper with a finger or a pencil. Also, teachers can give students templates for cutting out copies of some figures. These copies can then be moved around and super-imposed on the original figure. This process enables the student not only to identify the figure as embedded but also to determine how many positions the figure occupies within the larger figure.
Counting Squares
Draw the following figure on the chalkboard, or project on the overhead screen:

1. Tell students, "This is a 2×2 square. Pose the following questions:

   How many small squares do you see? [4]

   How many 2×2 squares do you see? [1]

   How many squares do you see altogether? [5]

2. Students can use their cutouts to show a 3×3 square. Pose the following questions:

   How many 1×1 squares do you see? [9]

   How many 2×2 squares do you see? [4]

   How many 3×3 squares do you see? [1]

   How many squares do you see altogether? [14]

3. Students can use their cutouts to show a 4&times4 square. Pose the following questions:

   How many 1×1 squares do you see? [16]

   How many 2×2 squares do you see? [9]

   How many 3×3 squares do you see? [4]

   How many 4×4 squares do you see? [1]

   How many squares do you see altogether? [30]

4. Ask students to look for a pattern in questions 1‑3. Make a prediction for the total number of squares in a 5×5 square. Students should test their predictions to find 55 squares total (25+16+9+4+1).
5. Return to the question posed at the beginning of class. "How many squares are on an 8×8 square checkerboard? Defend your answer."

The language in which students express their conclusions may vary from verbal to symbolic. For instance, for this problem some students may say, "You add up the square numbers until you get to the size of your big square"; other students will conclude that the number of squares in an n-by-n square is 1² + 2²  +...+n² and more advanced students may even recognize that this expression is equivalent to n(n+1)(2n+1)/6. All these responses should be valued.
Students may use a table to organize their data. For example, the following table may be created by students:

Size of Square	Number of Squares
1×1	64
2×2	49
3×3	36
4×4	25
5×5	16
6×6	9
7×7	4
8×8	1
TOTAL	204

Counting Rectangles
Once students have completed the Counting Squares activity, they may begin the next portion of the lesson.
Draw a figure similar to the one below on the chalkboard, or project on the overhead.

1. Tell students, "This figure is a 2 row × 3 column rectangle. How many of each type of rectangle can you find? Use your cutouts to help you answer these questions."

   1 row × 1 column [6]

   1 row × 2 column [4]

   1 row × 3 column [2]

   2 row × 1 column [3]

   2 row × 2 column [2]

   2 row × 3 column [1]

   How many total rectangles occur? [18]
2. Tell students to draw a 3 row × 4 column rectangle. Find the number of each type of rectangle. Organize the data in a table. Look for patterns. Find the total number of rectangles. [Students should identify 60 rectangles total.]
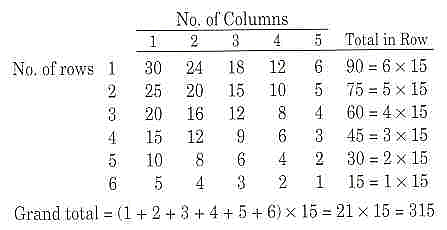
3. Ask students to predict the number of rectangles in a 6 row ×5 column rectangle. They should use the pattern found for the 3 row ×:4 column rectangle. Once again, they can use a table to organize their data. [Students should identify 315 rectangles.] Students’ tables may look like the one below:
   
4. Ask students to predict the number of rectangles in a 4×4 square. Students may create a table, similar to ones used previously in this lesson. [Students should identify 100 rectangles.]

Note: Some students may be reluctant to classify a square as a rectangle, which indicates that they are thinking at a lower van Hiele level than is assumed for high school-level geometry.
Counting Equilateral Triangles
Some students may finish sooner than others, so they may continue to the next activity in the lesson.
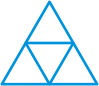
Draw the following figure on the chalkboard, or project on the overhead.

1. Ask students, "How many triangles are in this equilateral with side measuring 2 units?" [Students should identify 4 small, 1 large, or 5 total.]
2. Ask students, "How many triangles are in this equilateral triangle with side measuring 3 units?" Students may want to use their cutouts to help them. [Students should identify 9 small, 3 medium, and 1 large, for a total of 13 triangles.]
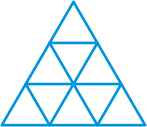
3. Students should use their answers to questions 1 and 2 to predict the number of triangles in an equilateral triangle with side measuring 4 units.
4. As a way of testing their predictions, students should look for patterns. They can count how many triangles of each size are in each of the triangles above. Consider triangles in both the up position and down position, as shown below: Students may create a table to organize their data. A sample table is shown below:
    
   

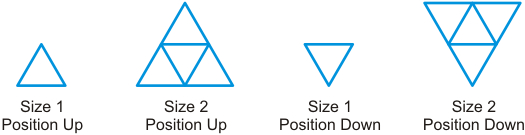
   Position	Size 1	Size 2	Size 3	Size 4
   Up	10	6	3	1
   Down	6	1	0	0
   Total	16	7	3	1

   GRAND TOTAL = 27 (16 + 7 + 3 + 1)  
5. Next ask students to create an equilateral triangle of size 5. Students can create a table, like the one below, to organize their data.   
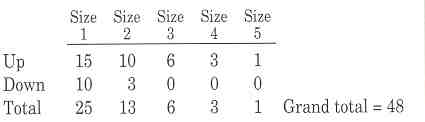
6. Students should predict the number of triangles in an equilateral triangle with side measuring 6 units. They should explain how they made their prediction. [All are triangular numbers.  For the up triangles the numbers will be 21, 15, 10, 6, 3, and 1. The down triangles will be 15 of size 1, 6 of size 2, and 1 of size 3. The pattern is found by counting down every other triangular number starting with the number found in the second column of the first row.]
7. Ask students, "What is the largest down triangle in an equilateral triangle with side measuring 8 units? [Down triangles can never be more than half the size of the large triangle. So the largest down triangle in a triangle measuring 8 units will be of size 4.] "In an equilateral triangle with side measuring 11 units?" [In a triangle measuring 11 units it will be of size 5.]
8. To close, ask students to explain how they would go about finding the number of triangles in an equilateral triangle with side measuring 10 units. [For the up triangles, find the first 10 triangular numbers. Listed backward, as they would appear in the table, they are 55, 45, 36, 28, 21, 15, 10, 6, 3, and 1. The down triangles follow the pattern of every other triangular number starting with 45: 45, 28, 15, 6, and 1. Check this result by observing that exactly 1 down triangle is of size 5. It is formed by joining the midpoints of the sides of the large triangle of size 10.]